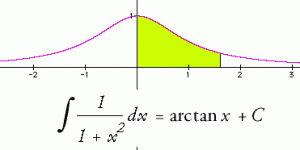
A análise matemática é o ramo da matemática que utiliza os conceitos introduzidos pelo cálculo diferencial e integral, e a sua ” génese ” emergiu pela necessidade de contribuir para a construção de fórmulas rigorosas às ideias de teor intuitivo do cálculo.
A disciplina de Análise Matemática, faz parte do ” curriculum” de muitas Instituições Universitárias e Politécnicas, estando presente em rigorosamente todos os cursos em que a matemática é a base dos mesmos ou a ciência matemática constitua ferramenta essencial para a resolução de problemas inter-correlacionados. São exemplos, todas as licenciaturas, mestrados e doutoramentos nas àreas da engenharia, da economia, da gestão empresarial, da matemática aplicada, da física, da química, entre outras. A disciplina análise matemática, nem sempre tem o mesmo nome em todas as Universidades e Institutos Politécnicos, sendo apelidada também por cálculo ou cálculo infinitesimal ou cálculo diferencial e integral ou matemáticas gerais, mas ” latus sensus” corresponde a programas semelhantes, se considerarmos o conjunto alargado de disciplinas de análise e que integram a análise matemática I, a análise matemática II, e em algumas Instituições mesmo a análise matemática III e IV.
A análise matemática é a disciplina, juntamente com álgebra e estatística que mais alunos do ensino superior tem procurado apoio no nosso Centro de Explicações e face ao qual nos sentimos orgulhosos, já que dispomos de vários Professores com competência inequívoca para esse auxílio.
Os explicadores do nosso Centro de Explicações estão aptos a apoiá-lo para compreender, funções reais de variável real, estudo de funções com variáveis independentes, derivada da função composta, derivada da função inversa, derivada da função implícita e derivada de funções definidas paramétricamente, derivadas parciais, primitivas e cálculo integral em |R, integrais múltiplos e integrais duplos, equações diferenciais de ordem 1 e superior, Series ( critério de comparação, Alambert, Cauchy, convergência, somas… etc ), polinómio de Taylor para funções… etc.
O insucesso escolar é uma realidade, mas o sucesso também.
Consulte os nossos preços acessíveis, contacte-nos e venha receber explicações de Análise Matemática. Ajudamos a preparar o seu sucesso.