Desenvolver competências de produção textual e capacidades de comunicação verbal na língua Inglesa é um dos vários objetivos que o Ministério de Educação propõe no programa curricular da disciplina de Inglês, num contexto de uma Europa, no sentido estrito e no mundo ” latus sensu” pluricultural e plurilingue.
A capacidade de comunicação com os cidadãos deste mundo global, revela-se não só um requisito basilar como um fundamento inalienável de educação cívica, democrática e humana.
A língua Inglesa tendo vindo cada vez mais a ganhar o estatuto de principal língua de comunicação entre os povos: nas tecnologias de informação, na
comunicação ciêntifica, nos negócios ou mesmo simplesmente na atividade turística dos cidadãos.
 O Quantum-Explicações propõe-se a ajudar os alunos a adquirir as ferramentas necessárias para utilizar a língua Inglesa não só na perspetiva de facultar oportunidades de contacto com realidades linguísticas diversificadas, mas também preparar os estudantes para o seu sucesso escolar na língua Inglesa, ampliando assim a capacidade de absorver conhecimentos que muitas vezes só são expostos na língua de William Shakespeare.
O Quantum-Explicações propõe-se a ajudar os alunos a adquirir as ferramentas necessárias para utilizar a língua Inglesa não só na perspetiva de facultar oportunidades de contacto com realidades linguísticas diversificadas, mas também preparar os estudantes para o seu sucesso escolar na língua Inglesa, ampliando assim a capacidade de absorver conhecimentos que muitas vezes só são expostos na língua de William Shakespeare.
Ler, ouvir, falar e escrever, integrando a dimensão sociocultural na interpretação e produção de texto, por parte do aluno na utilização da língua Inglesa ( a palavra, a frase, a prosódia ) e tendo como pano de fundo as macrofunções do discurso, os tipos de texto e as intenções de comunicação.
Para o ensino secundário em particular, no domínio da interpretação os alunos devem ler ( compreender diversos tipos de texto – textos curtos , extensos, literários ou não literários ) e ouvir ( compreender o discurso fluido e acompanhar linhas de argumentação ).
No domínio da produção os estudantes devem falar ( interagir com eficácia na língua Inglesa participando no diálogo e defendendo os seus pontos de vista ) e escrever ( elaborando textos de forma estruturada e com capacidade de síntese mobilizando conhecimentos adquiridos )
Consulte neste site os nossos preços e contacte-nos, pois temos respostas pedagógicas para si.



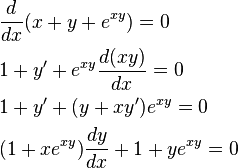

 tivo potenciar os alunos a utilizar conhecimentos básicos de álgebra linear e de cálculo, aplicando-os na resolução de problemas biológicos.
tivo potenciar os alunos a utilizar conhecimentos básicos de álgebra linear e de cálculo, aplicando-os na resolução de problemas biológicos. 





