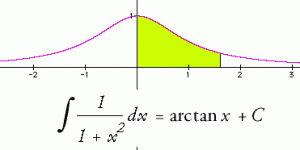
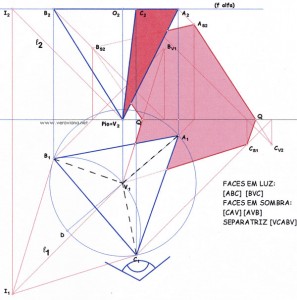
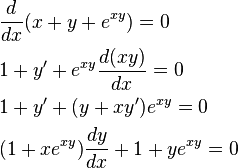A matemática continua a ser uma disciplina em que grande parte dos alunos enfrenta dificuldades acrescidas.
Este fenómeno não é apenas, sensível no universo escolar Português e abrange genericamente os alunos das escolas de quase todo o mundo (embora no nosso país esse fenómeno seja mais marcante), nomeadamente, nos países desenvolvidos ou em vias de desenvolvimento.
Segundo as estatísticas oficiais, na União Europeia, 23% dos alunos do ensino básico, 68% dos alunos do ensino secundário e 31% dos estudantes do ensino superior, nos grandes centros urbanos, recebem explicações clássicas ou algum apoio complementar, no âmbito dos conhecimentos matemáticos.
As explicações presenciais e individuais em sala, são a melhor forma de ajudar os alunos a assimilarem com crítérios consolidados e pedagógicos, o conjunto de conceitos abstratos, porque numéricos, que refletem realidades insofismáveis.
porque numéricos, que refletem realidades insofismáveis.
A matemática requer por parte do aluno a apreensão sólida de conhecimentos teóricos que devem ser posteriormente testados ( cimentados ) em utilizações práticas, isto é, a matemática necessita de pesquisa “laboratorial”.
Uma das formas erróneas, inscritas na pedagogia oficial do ensino da matemática a alguns anos a esta parte, tem sido a ” facilitação ” dos raciocínios, nomeadamente os raciocínios lógicos, enquadrando as experiências de jogos, meramente como interpretações de realidades, muito valorativas dos comportamentos e pouco adaptadas ao raciocínios em contextos ciêntifico-sociais.
Por outro lado, esta facilitação do ensino de matemática, levaram os professores a utilizarem metodologias que repeliam e persistem ainda um pouco a repelir, o exercício de memorização, quando o treino de memorização, também, é essencial à nossa realidade objetiva.
Neste domínio, é exemplificativo, a permissão em sala de aula e fora dela, das máquinas de calcular, para resolução de problemas matemáticos, logo em tenra idade, como acontecia no 1º ciclo e 2º ciclo ( cálculos aritméticos) ou mesmo já no 3º ciclo ( para ajuda a cálculos matemáticos ).
A despeito da situação ter melhorado um pouco nos últimos anos, estamos longe, de um ensino-aprendizagem da matemática eficiente.
Essa realidade é ainda mais visível, quando alunos do 9º ano, com notas relativamente satisfatórias, ao passarem para o 10º ano de escolaridade, tem abruptamente classificações negativas.
De facto a partir do ensino secundário o conteúdo programático e a exigência de conhecimentos da ciência matemática já não é tão facilitador e o impacto na consistência das bases de matemática (que deveriam estar cimentadas no ensino básico) é muito forte.
As explicações de matemática tem um papel muito importante na aquisição dos saberes, pois substituem (em todo o mundo), um ensino massificado na escola por um ensino personalizado e atendível às necessidades de competência específicas de um aluno concreto ( que não de uma turma).
O Quantum-explicações, ministra explicações de matemática, no sentido clássico e com excelente sucesso dos seus explicandos, por isso dizemos que temos respostas pedagógicas para si. Contacte-nos e informe-se sobre os nossos preços acessíveis para explicações de matemática do 1º ciclo, 2º ciclo, 3º ciclo e ensino secundário.