EXPLICAÇÕES LISBOA - 912 473 571 » Tag » Matemática

Tag Archives: Matemática

Explicações de Matemática ao 12º ano

By | |
Leave a comment

A palavra “Matemática” tem origem na palavra grega “máthema” que significa Ciência, conhecimento ou aprendizagem, derivando daí “mathematikós”, que significa o prazer de aprender.

125 Em ano de exames nacionais de matemática, os professores do Centro de Explicações de Lisboa, irão fornecer uma ajuda decisiva para que haja prazer em aprender matemática, ajudando os alunos a compreender e a proceder aos respetivos cálculos, inerentes ao conteúdo programático da disciplina para o 12º ano, definido pelo Ministério de Educação, nomeadamente; combinações, arranjos, probabilidades, axiomática dos conjuntos, probabilidade condicionada, triângulo de Pascal, binómio de Newton, regra de Laplace, funções logarítmicas, funções exponenciais. limite de função segundo Heine, propriedades operatórias, sobre limites, limites notáveis, levantamento de indeterminações, continuidade e teorema de Bolzano-Cauchy, funções derivaveis, regras operatórias de derivação, estudo de funções ( crescimento, decrescimento e concavidades, máximos, mínimos e continuidades ), introdução às primitivas e integrais, números complexos, conversão de números complexos na forma algébrica para a forma trigonométrica e da trigonométrica para a algébrica, operações com números complexos, domínio planos e condições em variável complexa.

Consulte os nossos preços e contacte-nos, temos respostas pedagógicas para superar as dificuldades na disciplina de matemática durante o ano letivo ( testes e avaliações) e prepará-lo para o exame nacional.

(3) Ciêntistas, pensadores e artistas que mudaram o mundo

By | | ,
Leave a comment
“Nós movemo-nos de mais por suposições mais ou menos plausiveis, mas realmente arbitrárias, para conclusões  demonstrativas, elegantes, mas irrelevantes.”

Wassily Leontief (1905 – 1999)

Wassily Leontief

Wassily Wassilyovitch Leontief , foi um economista Russo, que emigrou para os Estados Unidos da América em 1931, onde se naturalizou.

Foi notável por pesquisas sobre como as mudanças em um único setor da economia afetam os demais.

Recebeu o prémio Nobel das Ciências Económicas em 1973, pelo desenvolvimento da matriz de input-output, conhecida como a “matriz de Leontief” e a sua aplicação à economia. Este modelo foi apresentado pela primeira vez no seu livro The Structure of the American Economy, publicado no ano de 1941. O modelo tornou-se um instrumento essencial no planeamento, tanto nas economias de mercado como nas economias de direção central.

Do ponto de vista das correntes de pensamento económico, Leontief foi um destacado Keynesiano, com grande influência sobre os neo-keynesianos e os contêmporâneoas das teorias de David Ricardo.

Torbern Olof Bergman (1735 – 1784 ) foi um químico Sueco. Também são conhecidas contribuições importantes deste ciêntista na física, minorologia na astronomia e geologia, mas foi, de facto, na química que mais se notabilizou.

Torbem Olof Bergman em 1777, propôs a criação de um novo ramo da química: a química orgânica. Esta nova vertente da química teria como objeto de estudo os compostos extraídos dos organismos vivos.Torbem Olof Bergman

Torbern Bergman, introduziu a nomenclatura binomial dos sais e é o percursor de uma classificação química dos minerais, baseada na composição química.

Torbem Olof Bergman

A química analítica teve importante desenvolvimento com os trabalhos de Bergman, que separou os metais ( cátions) em grupos, dando origem à análise química sistemática.

É freqüentemente considerado como o fundador da análise inorgânica quantitativa e um dos fundadores da mineralogia química.Bergman desenvolveu um esquema de classificação dos minerais que se baseava nas características químicas e na aparência.Salientam-se as suas pesquisas sobre química dos metais nomeadamente do bismato e do níquel.Desenvolveu métodos quantitativos para determinar o chumbo, o ácido sulfúrico e o cálcio.Identificou o manganês, isolou o tungsténio e obteve, por oxidação do açucar, o ácido oxálico.Estudou a química do alume.Introduziu a ideia de proporções de combinação constantes.Desenvolveu uma teoria reticular dos cristais.

 ” Só sei, que nada sei “

“Sócrates ( 469 AC – 399 AC )

Sócrates, foi um filósofo de Atenas e um dos mais importantes ícones da tradição filosófica ocidental.Foi o professor de Platão um dos filósofos mais influentes de todos os temposÉ considerado por muitos como o filósofo dos filósofos.Não são conhecidos escritos e o pensamento de Sócrates é nos legado por Platão.Sócrates não valorizava os prazeres dos sentidos, todavia se escalava o belo entre as maiores virtudes, junto ao bom e ao justo. Dedicava-se ao parto das ideias dos cidadãos de Atenas, mas era indiferente em relação aos seus próprios filhos.Sócrates

O método socráticoconsiste numa técnica de investigação filosófica, que faz uso de perguntas simples e quase ingênuas que têm por objetivo, em primeiro lugar, revelar as contradições presentes na atual forma de pensar do aluno, normalmente baseadas em valores e preconceitos da sociedade, e auxiliá-lo assim a redefinir tais valores, aprendendo a pensar por si mesmo.

Sócrates

Sócrates dizia que sua sabedoria era limitada à sua própria ignorância. Segundo ele, a verdade, escondida em cada um de nós, só é visível aos olhos da razão. (daí a célebre frase “Só sei que nada sei”!).Ele acreditava que os erros são consequência da ignorância humana. Nunca proclamou ser sábio. A intenção de Sócrates era levar as pessoas a conhecerem seus desconhecimentos (“Conhece-te a ti mesmo”.). Através da problematização de conceitos conhecidos, daquilo que se conhece, percebe-se os dogmas e preconceitos existentes.

 

 “Todo o nosso conhecimento se inicia com sentimentos.”

Leonardo da Vinci (1452 – 1519),

 

Leonardo di Ser Piero da Vinci, foi uma das figuras mais importantes do renascentismo e destacou-se  como escultor, cientista, matemático, pintor, engenheiro, inventor, anatomista, arquiteto, botânico, entre outras ( poeta e músico)

Leonardo da Vinci é conhecido principalmente como pintor, sendo duas de suas obras, a Mona Lisa e  A última ceia,  as pinturas mais famosas, mais reproduzidas de todos os tempos.

Leonardo é também referenciado pela sua engenhosidade tecnológica; concebeu ideias muito avançadas para o seu tempo, como um protótipo de helicóptero, um tanque de guerra, o uso da energia solar, uma calculadora, o casco duplo nas embarcações, e uma teoria rudimentar das placas tectônicas.

Leonardo da Vinci

Algumas de suas invenções menores, como uma bobina automática, e um aparelho que testa a resistência à tração de um fio, entraram sem crédito algum para o mundo da indústria.

Como cientista, foi responsável por grande avanço do conhecimento nos campos da anatomia, da engenharia civil, da óptica e da hidrodinâmica.

Leonardo da Vinci é considerado por vários estudiosos, o maior gênio da história da humanidade, devido a sua multiplicidade de talentos para ciências e artes e a sua engenhosidade e criatividade, para além de suas obras polêmicas.

(2) Ciêntistas e artistas que mudaram o mundo

By | | ,
Leave a comment
“Todos os efeitos da natureza não passam de resultados matemáticos de um número restrito de leis imutáveis”

Pierre Simon Laplace ( 1749 – 1827)

Pierre Laplace

Pierre Simon, Marquis de Laplace, nasceu em Paris, e foi um matemático, físico e astrónomo Francès, que deu corpo à sistematizaçãoe ampliação  da astronomia matemática. A obra-prima “Mecànica Celeste”, que escreveu, traduziu o estudo geométrico da mecânica clássica utilizada por Newton para um estudo baseado em cálculo matemático, conhecido como física mecânica.Recebeu o seu nome, a regra de Laplace, no domínio do cálculo da probabilidade ( em que relaciona o número dos casos favoráveis de um acontecimento, com o número de casos possíveis, cuja a aprendizagema os alunos em Portugal é transmitida no ensino secundário).Pierre Laplace, também formulou a equação de Laplace e a transformada de Laplace que é utilizada em todos os ramos da matemática e física, bem como o operador diferencial de Laplace, contributo muito importante na matemática aplicada.

 

“Um verdadeiro conservacionista é um homem que sabe que o mundo não é dado pelos seus pais, mas emprestado de seus filhos”

John James Audubon (1785- 1851)

 

John James Audubon, foi um naturalista Americano, com origem Francesa que promoveu a ilustração científica de aves. Realizou vários trabalhos nesse

John Audubon

contexto ciêntifico, sendo o mais conhecido o ” The Birds of America”. que alcançou, durante a sua vida, um indejével sucesso comercial e trouxe-lhe enorme popularidade junto do público. O prestígio científico alcançado pela obra valeu-lhe elogios rasgados dos seus pares e permitiu-lhe tornar-se o segundo americano a ser incluido na prestigiante Royal Society britânica para as ciências.

 

 

“A verdade é que antes a física era mais simples, harmônica e, portanto, mais satisfatória!”

( A física determinista até Newton e depois de Newton )

Max Plank  (1858 – 1947)

Max Karl Ernst Ludwig Planck, nasceu na Alemanha e foi o físico considerado o pai da física quântica, ao descobrir o ” buraco negro”. Max Plank é um dos cientistas mais importantes do século XX, tendo sido agraciado com o prémio Nobel da física em 1918, pela sua contribuição para a física quântica.

Max Plank, desenvolveu trabalhos sobre a teoria do calor, tendo descoberto em seguida o formalismo termodinâmico.

Em fins do século XVIII, uma das dificuldades da física consistia na interpretação das leis que governam a emissão de radiação por parte dos corpos negros. Tais corpos são dotados de alto coeficiente de absorção de radiações; por isso, parecem negros para a vista humana.

Ao pesquisar as radiações eletromagnéticas descobriu a nova cosnatante fundamental, a “constante de Plank”, que é utilizada para calular a energia do fóton ( quantum) e a lei da radiação térmica, chamada a “lei de Plank da radiação”.

Essa foi a base da teoria quântica, também com a colaboração de Albert Einstein e de Niels Bohr, os quais trabalharam juntos na Universidade de Berlim.

Max Plank

Einstein  foi o primeiro a afirmar que a teoria quântica era revolucionária. Em 1909, Einstein sugeriu numa conferência que era necessário encontrar uma forma de entender em conjunto ondas e partículas. No entanto, na década de 1920, quando a teoria quântica original foi substituída pela nova mecânica quântica, Einstein discordou da interpretação de Copenhaga, porque ela defendia que a realidade era probabilística e aleatória. Einstein concordava que a mecânica quântica era a melhor teoria disponível, mas procurou sempre uma explicação determinista, isto é não-probabilística

É deste período de investigação a famosa frase de Einstein ” Deus não joga dados “.

As descobertas de Planck, que mais tarde viriam a ser confirmadas por outros cientistas, foram o nascimento de um campo totalmente novo na física moderna (pós Newton), conhecidos como mecânica quântica, e que forneceram a base para a investigação de áreas pouco exploradas até então, como a energia nuclear.

“Um homem a quem foi dada a oportunidade de abençoar o mundo com uma grande idéia criativa não precisa do louvor da posteridade. Sua própria façanha já lhe conferiu uma dádiva maior!”               Albert Einstein, sobre Max Planck

↓
” Na vida, os blocos de granito afundam, já as cascas das àrvores continuam flutuando”

Pierre-Auguste Renoir (1841-1919)

Pierre Auguste Renoir, de naturalidade Frnacesa, foi um dos mais célebres pintores e um dos mais emblemáticos nomes do movimento artístico impressionista.

Apesar de sua técnica ser essencialmente impressionista, Pierre Renoir nunca deixou de dar importância à forma – de fato, teve um período de rebeldia diante das obras de seus amigos, no qual se voltou para uma pintura mais figurativa, evidente na longa série Banhistas. Mais tarde retomaria a plenitude da cor e recuperaria sua pincelada enérgica e ligeira, com motivos de beleza e sensualidade, como ” A adormecida”.

Pierre Renoir

A sua obra de maior impacto é Le Moulin de la Galette, em que conseguiu elaborar uma atmosfera de vivacidade e alegria à sombra refrescante de algumas árvores, aqui e ali intensamente azuis. Percebendo que traço firme e riqueza de colorido eram coisas incompatíveis, Renoir concentrou-se em combinar o que tinha aprendido sobre cor, durante o seu período impressionista, com métodos tradicionais de aplicação de tinta. O resultado foi uma série de obras-primas, conhecidas em todo o mundo.

(1) Cientistas e pensadores que mudaram o mundo

By | | ,
Leave a comment

“Ninguém é tão grande que não possa aprender, nem tão pequeno que não possa ensinar”

Píndaro (522 AC . 443 AC)

pindaro

Píndaro, também conhecido como Píndaro de Cinoscefale ou Píndaro de Beozia, foi um poeta Grego, autor de “Epinícios” ou “Odes Triunfais”, e autor também da célebre frase “Homem, torna-te no que és”.São, até hoje, conhecidos 45 epinícios, divididos em quatro livros, conforme o nome dos jogos que celebravam: Olímpicas, Píticas, Neméias e Ístmicas.

 

“Não é o mais forte que sobrevive, nem o mais inteligente, mas o que melhor se adapta às mudanças.”

Charles Darwin  (1809 – 1882)

Charles Robert Darwin, foi um Biólogo Inglês, que alcançou fama ao convencer a comunidade científica, de uma teoria explicativa da evolução dos seres vivos com base.na seleção natural e sexual. O desenvolvimento desta teoria permitiu, o que é agora, considerado o paradigma central para explicação de diversos fenómenos na Biologia.

darwin

Escreveu vários livros e artigos científicos, como ” A origem das espécies ” ( 1859 ) ), A descendência do Homem e seleção em relação ao sexo ” ( 1871), e a ” Expressão da emoção em Homens e animais ” (1872). Ingressou na Royal Society e recebeu diversos prémios na época.

 

“Duas coisas são infinitas: o universo e a estupidez humana. Mas, no que respeita ao universo, ainda não adquiri a certeza absoluta.”

Albert Einstein (1879 – 1955)

Albert Einstein , foi um físico alemão, nascido em Ulm, Baden-Württemberg ( capital de Estado – Estugarda) filho de uma família judaica e tornou-se mundialmente famoso pela sua formulação da teoria da relatividade. Foi prémio Nóbel da Física em 1921, pela precisão com que descreveu cientificamente o efeito fotomagnético.

O trabalho cientifico que realizou, possibilitou a criação da energia atómica e muitos outros desenvolvimentos científicos, posteriores.

Albert Einstein

É considerado um génio, tendo cem físicos de renome mundial, em 2009, considerado Albert Einstein como o mais memorável físico de todos os tempos.Embora tenha nascido na Alemanha, viveu em Itália ( Milão), na Suíça e nos Estados Unidos da América.Publicou muitos artigos em revistas cientificas, inicialmente, artigos sobre mecânica estatística.

Em 1905, Albert Einstein, submete quatro artigos cruciais o primeiro propondo a hipótese do quanta de luz, o segundo sobre o movimento Browniano, cujas leis contribuíram para a realidade física dos átomos, o terceiro sobre a electrodinâmica dos corpos em movimento, o qual introduz a teoria da relatividade restrita e por último sobre a consequência importante desta teoria, a inércia da energia ou E=mc2, talvez a equação mais conhecida da física.

A abordagem de Einstein em todos estes artigos tinha algo em comum: como ele explicou mais tarde, os seus trabalhos inseriam-se nas chamadas “teorias de princípio”.

 

“ Si cogito, ergo sum” (Se penso, logo existo)”

René Descartes (1596 – 1650)

René Descartes, foi um filósofo, físico e matemático Francês. Notabilizou-se sobretudo por seu trabalho revolucionário na filosofia, mas também obteve reconhecimento no âmbito da ciência matemática por sugerir a fusão da geometria com a álgebra, gerando a geometria analítica e o sistema de eixos coordenados, sistema, que hoje é conhecido pelo seu nome ( sistema de eixos cartesianos).

René Descartes

Descartes, por vezes chamado de “o fundador da matemática e filosofia modernas” é considerado um dos mais importantes e influentes pensadores da História do Pensamento Ocidental.

 

 

 

“Não há nada na nossa inteligência que não tenha passado pelos sentidos.”

Aristóteles (384 AC – 322 AC)

 

Aristóteles

Aristóteles, foi um filósofo Grego, aluno de Platão e professor de Alexandre, o Grande.Aristóteles é considerado como um dos fundadores da filosofia moderna e tem escritos que abrangem temas, como a física, a metafísica, a música, as leis da poesia e do drama, a retórica, a ética, o governo, a biologia e a zoologia.

No que diz respeito às ciências físicas influenciou profundamente o cenário intelectual medieval, e esteve presente até o Renascimento – embora eventualmente tenha vindo a ser substituído pela física newtoniana. Nas ciências biológicas, a precisão de algumas de suas observações foi confirmada apenas no século XIX. Nas suas obras pode ser encontrado o primeiro estudo formal conhecido da lógica, que foi incorporado posteriormente à lógica formal. Na metafísica, o aristotelismo teve uma influência profunda no pensamento filosófico e teológico nas tradições judaico-islâmicas durante a Idade Média, e continua a influenciar a teologia cristã, especialmente a ortodoxa oriental, e a tradição escolástica da Igreja Católica. O seu estudo da ética, embora sempre tenha continuado a ser influente, conquistou um interesse renovado com o advento moderno da ética da virtude.

Análise Vetorial e Equações Diferenciais

By | |
Leave a comment

O Cálculo vetorial, é uma área da matemática relacionada com a análise real multivariável de vetores em duas ou mais dimensões.

Equações diferenciais são equações cuja incógnita é uma função que aparece na equação sob a forma das respectivas derivadas. Dada uma variável x, função de uma variável y, a equação diferencial envolve, x, y, derivadas de y e eventualmente também derivadas de x.

O domínio dos conceitos de limite, continuidade e diferenciabilidade de campos escalares e vetoriais, bem como o cálculo de integrais múltiplos e a resolução de equações diferenciais lineares de coeficientes constantes ou modelar situações reais usando campos escalares e/ou vectoriais são entre outras, exigências para obter sucesso nesta “ cadeira”.

Os explicadores da Quantum-Explicações, irão ajudar a ultrapassar

as dificuldades inerentes a muitas questões dos alunos, como, a

título de exemplo:

– matriz jacobiana. – Derivada da função composta. – Integrais duplos. Teorema de Fubini – Mudança de variáveis em integrais duplos; transformações lineares e coordenadas polares. – Integrais triplos. – Integrais de superfície. Representação paramétrica. – Integral de superfície de campos escalares. Propriedades. Aplicações. – Equações Diferenciais Ordinárias.

Veja os nossos preços e contacte-nos, pois temos soluções para o seu sucesso.
 

Explicações de Álgebra Linear

By | |
Leave a comment

A álgebra é o ramo da matemática que estuda as aplicações formais de equações, operações matemáticas, estruturas algébricas e polinómios e apresenta-se como uma disciplina (conhecimento) independente em muitos cursos do ensino superior, universitário e politécnico.

A álgebra surgiu no Egipto quase ao mesmo tempo que na Babilônia; mas faltavam à álgebra egípcia, segundo Papiro Moscou e o Papiro Rhind (documentos egípcios datados respetivamente de cerca de 1850 a.C. e 1650 a.C), os métodos sofisticados da álgebra babilônica, bem como a variedade de equações resolvidas.

O sistema de numeração egípcio, relativamente primitivo em comparação com o dos babilônios, ajuda a explicar a falta de sofisticação da álgebra egípcia. Os matemáticos europeus do século XVI tiveram de estender a noção indo-arábica de número antes de poderem avançar significativamente, para além dos resultados babilônios de resolução de equações.

A álgebra, lecionada,  introduz o conceito de variável como representação de números, utilizando expressões em que estas variáveis são manipuladas através de regras operatórias aplicáveis a números, como a multiplicação e a adição.

Estes conceitos permitem, nomeadamente resolver equações.

Contudo a adição e a multiplicação podem ser generalizadas, permitindo as suas  definições exactas conduzirem-nos a estruturas, nomeadamente os conhecidos anéis, grupos e corpos, que são estudados na álgebra abstrata.

Os professores do Centro de Explicações de Lisboa, tem respostas pedagógicas para si, ajudando-o a desvendar os segredos da álgebra, explicando conceitos e cálculos :

  • Matrizes, sistema de equações lineares e determinantes ( conceito de matriz, cálculo do deteminante, desenvolvimento de Laplace, matrizes adjuntas e inversas, matriz identidade, propriedades operatórias, fórmula de Gauss-Jordan … etc)
  • Espaços e subespaços vetoriais ( conbinações lineares, dependência e independência linear, base de um espaço vetorial, mudança de base …etc )
  • Transformações lineares ( conceitos e teoremas, transformações do plano no plano …etc)
  • Valores e vectores próprios ( polinómio característico, … diagonalização de operadores, produto interno, tipos especiais de operadores lineares ), entre outros …

O nosso quadro de professores licenciados, mestres e doutorados oferecem-lhe as condições ” sine qua none ” do seu sucesso na cadeira de Álgebra Linear.

Navegue neste site e contacte-nos

Explicações de Estatística Lisboa

By | |
2 Comments

À ciência que dispõe de processos apropriados para recolher, organizar, classificar, apresentar e interpretar conjuntos de dados, apelidamos de Estatística.

A Estatística permite extrair informação dos dados por forma a  obter uma melhor compreensão das situações que representam uma determinada realidade.

O Quantum – Centro de Explicações de Lisboa, ministra explicações de estatística, também denominada de ” Probabilidade e Estatística ” em algumas Instituições do ensino superior em Portugal, nomeadamente no IST – Instituto Superior Técnico ou na FCT – Faculdade de Ciências e Tecnologias da Universidade Nova de Lisboa.

A absorção de conceitos fundamentais, a capacidade de manuseamento dos dados e a utilização de cálculos para engendar respostas são essenciais na estatística.

Por isso. os explicadores ( licenciados, mestres ou doutorados) do nosso Centro de Explicações, transmitirão aos estudantes conhecimentos que viabilizem a aprendizagem da estatística, desde os elementos mais básicos, alguns já apreendidos no ensino secundário (espaço de resultados, acontecimentos, acontecimentos independentes … ) até aos mais complexos (axiomática de Kolmogorov, variáveis aleatórias das funções de distribuição, função geradora de momentos,  valor esperado e momentos de variáveis aleatórias bidimensionais, inferência estatística), distribuições discretas ( distibuições de Bernoulli e de Poisson) ou distibuições contínuas ( distribuições normal, exponencial, Gama, quiquadrado, teorema do limite central).

Modelo de regressão linear

Estas são normalmente as temáticas, genéricas, dos conteúdos programáticos das cadeiras de estatística de primeiro ano nas Instituições de ensino superior. Contudo, a ciência estatística, não se dissolve nos temas acima referenciados e em muitas Instituições universitárias os programas curriculares da cadeira de estatística ( frequentemente chamada de estatística II e mesmo de estatística III nos cursos de licenciatura) contemplam outras matérias de desenvolvimento, abordando a estimação, os testes de hipóteses, modelos não paramétricos, modelos de regressão linear e complementos a este modelo.

Em alguns cursos de mestrado com forte componente matemática e mesmo em doutoramento estudam-se conteúdos de estatística avançada e  processos estocásticos.

A necessidade de formular  políticas públicas por por parte do Estado, está na origem da estatística, já que a recolha, organização e tratamento de dados concernentes aos elementos de teores económicos, demográficos e de administração pública eram e são importantes para a criação dessas políticas.

No primeiro quatil do século XIX registou-se um incremento da abrangência da utilização da estatística ao incluir a acumulação e análise de dados, sendo hoje a estatística amplamente aplicada nas ciências naturais e nas ciências sociais inclusive na administração pública e gestão privada das organizações e empresas “stritus sensus”.

Os fundamentos matemáticos construídos no século XVII com o desenvolvimento da teoria das probabilidades por Pascal e Fermat e o método dos mínimos quadrados, descrito pela primeira vez por Carl Gauss e o uso dos computadores da era contemporânea permitiram a computação dos dados estatísticos em larga escala, possibilitando novos métodos, antes julgados impossíveis.

Navegue no nosso site, consulte os nossos preços acessíveis, peça mais esclarecimentos e aceite a ajuda dos nossos explicadores, contactando-nos, pois queremos ser parte do seu sucesso nas cadeiras de estatística.

Explicações de Matemática para Biólogos

By | |
Leave a comment

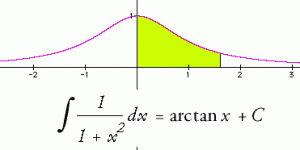
A cadeira de Matemática para Biólogos, ministrada, nomeadamente na Faculdade de Ciências da Universidade de Lisboa, tem como objetivo potenciar os alunos a utilizar conhecimentos básicos de álgebra linear e de cálculo, aplicando-os na resolução de problemas biológicos. A unidade curricular incide fundamentalmente em conhecimentos e técnicas de resolução de problemas utilizando o cálculo matricial, a derivação, as primitivas e integrais para além das equações diferenciais.

Decida ultrapassar, definitivamente, as dificuldades na cadeira de matemática para biólogos junto dos nossos explicadores, tendo o sucesso que necessita.

 

Explicações de Matemática

By | |
Leave a comment

A matemática continua a ser uma disciplina em que grande parte dos alunos enfrenta dificuldades acrescidas.

Este fenómeno não é apenas, sensível no universo escolar Português e abrange genericamente os alunos das escolas de quase todo o mundo (embora no nosso país esse fenómeno seja mais marcante), nomeadamente, nos países desenvolvidos ou em vias de desenvolvimento.

Segundo as estatísticas oficiais, na União Europeia,  23% dos alunos do ensino básico, 68% dos alunos do ensino secundário e 31% dos estudantes do ensino superior, nos grandes centros urbanos, recebem explicações clássicas ou algum apoio complementar, no âmbito dos conhecimentos matemáticos.

As explicações presenciais e individuais em sala, são a melhor forma de ajudar os alunos a assimilarem com crítérios consolidados e pedagógicos, o conjunto de conceitos abstratos, porque numéricos, que refletem realidades insofismáveis.

A matemática requer por parte do aluno a apreensão sólida de conhecimentos teóricos que devem ser posteriormente testados ( cimentados ) em utilizações   práticas, isto é, a matemática necessita de pesquisa “laboratorial”.

Uma das formas erróneas, inscritas na pedagogia oficial do ensino da matemática a alguns anos a esta parte,  tem sido a  ” facilitação ” dos raciocínios, nomeadamente os raciocínios lógicos, enquadrando as experiências de jogos, meramente como interpretações de realidades, muito valorativas dos comportamentos e pouco adaptadas ao raciocínios em  contextos ciêntifico-sociais.

Por outro lado, esta facilitação do ensino de matemática, levaram os professores a utilizarem metodologias que repeliam e persistem ainda um pouco a repelir, o exercício de memorização, quando o treino de memorização, também, é essencial à nossa realidade objetiva.

Neste domínio, é exemplificativo, a permissão em sala de aula e fora dela, das máquinas de calcular, para resolução de problemas matemáticos, logo em tenra idade, como acontecia no 1º ciclo e 2º ciclo ( cálculos aritméticos) ou mesmo já no 3º ciclo ( para ajuda a cálculos matemáticos ).

A despeito da situação ter melhorado um pouco nos últimos anos, estamos longe, de um ensino-aprendizagem da matemática eficiente.

Essa realidade é ainda mais visível, quando alunos do 9º ano, com notas relativamente satisfatórias, ao passarem para o 10º ano de escolaridade, tem abruptamente classificações  negativas.

De facto a partir do ensino secundário o conteúdo programático e a exigência de conhecimentos da ciência matemática já não é tão facilitador e o impacto na consistência das bases de matemática (que deveriam estar cimentadas no ensino básico) é muito forte.

As explicações de matemática tem um papel muito importante na aquisição dos saberes, pois substituem (em todo o mundo), um ensino massificado na escola por um ensino personalizado e atendível às necessidades de competência específicas de um aluno concreto ( que não de uma turma).

O Quantum-explicações, ministra explicações de matemática, no sentido clássico e com excelente sucesso dos seus explicandos, por isso dizemos que temos respostas pedagógicas para si. Contacte-nos e informe-se sobre os nossos preços acessíveis para explicações de matemática do 1º ciclo, 2º ciclo, 3º ciclo e ensino secundário.

Explicações de Análise Complexa e Equações Diferenciais

By | |
Leave a comment

Uma equação diferencial é aquela em que a função incógnita surge sob a forma da sua respetiva derivada. Os fundamentos das equações diferenciais estão tão dominados pelas contribuições do matemático Leonhard Euler, que sentimos quase um impulso em afirmar que a história desta temática começa e termina com ele. Mas obviamente que isso, seria uma simplificação grosseira do seu desenvolvimento. Existem vários contribuintes importantes, e aqueles que vieram antes de Euler foram necessários para que ele pudesse entender o cálculo e a análise, necessários para desenvolver muitas das ideias fundamentais.

Análise Complexa e Equações Diferenciais

Com efeito, as equações diferenciais começaram com os inventores do cálculo, Newton, Fermat e Leibniz, já que são estes os brilhantes matemáticos que procederam à descoberta para a derivada, que de forma subsequente apareceu em equações. No entanto as equações diferenciais, se exceptuarmos as equações separáveis eram e ainda hoje são difíceis de resolver se não dominarmos técnicas próprias de resolução. O método de separação das variáveis foi desenvolvido por Jakob Bernoulli e generalizado por Leibniz a partir da integral ( antiderivada).

Outros matemáticos deram contribuições relevantes nesta área, como são os exemplos de Joseph Lagrange ( mostrou que a solução geral de uma equação diferencial linear homogénea de grau n é uma combinação linear de n soluções independentes), joseph Fourrier ( resolve a equação diferencial parcial – series de Fourrier), Legrende. Hankel, Bessel, Chebyshev, Hermite ( resolução de equações diferenciais ordinárias), Gauss e Cauchy ( desenvolvimento do conceito de funções de variáveis complexas), Laplace ( melhor entendimento das técnicas numéricas e da integração), etc .

Muitos dos alunos , apresentam  algumas dificuldades no entendimento do conteúdo programático desta unidade curricular .

Os professores ( mestres , doutorandos e doutorados ) do nosso Centro de Explicações, poderão ser uma

Leonhard Euler

 

ajuda relevante para o seu sucesso na  “cadeira“  de Análise Complexa e Equações Diferenciais, permitindo a compreensão das coordenadas polares, séries numéricas e de potência, funções harmónicas e núcleo de Poisson, integrais de linha,  funções  C  diferenciáveis, regra de derivação, fórmulas integrais de Cauchy, fórmula de Taylor, integrais de variável real, integrais impróprios, transformada de Laplace e a resolver equações e muito mais …

Contacte-nos, temos respostas pedagógicas para si.

Equação diferencial

 

ORDEM DE UMA EQUAÇÃO DIFERENCIAL:  é a ordem da mais alta derivada que nela aparece.

GRAU DE UMA EQUAÇÃO DIFERENCIAL: considerando as derivadas como um polinómio, é o grau da derivada de mais alta ordem que nela aparece.

SOLUÇÃO OU INTEGRAL GERAL: é toda a função que verifica, identicamente, a equação diferencial e vem expressa em termos de n constantes arbitrárias. Se a equação é de primeira ordem, aparece uma constante, se é de segunda ordem, duas constantes, etc..